Differentiation 1
Differentiation is a method for calculating the gradient of a curve at a given point. On this sheet, we recap the definition of the derivative of a function in one variable and practice the method of differentiation from first principles.
We will also revise the standard formula for the derivative of a power, and practice using it to differentiate polynomials. The problem set at the end of this resource includes some contextual questions to give a taste of how differentiation can be used to solve problems in the real world.
First Principles Differentiation
Definition 1.
The derivative of a function at a point on the curve is
| (1) |
The rationale for this formula is the following: suppose is a second point on the curve, very close to .
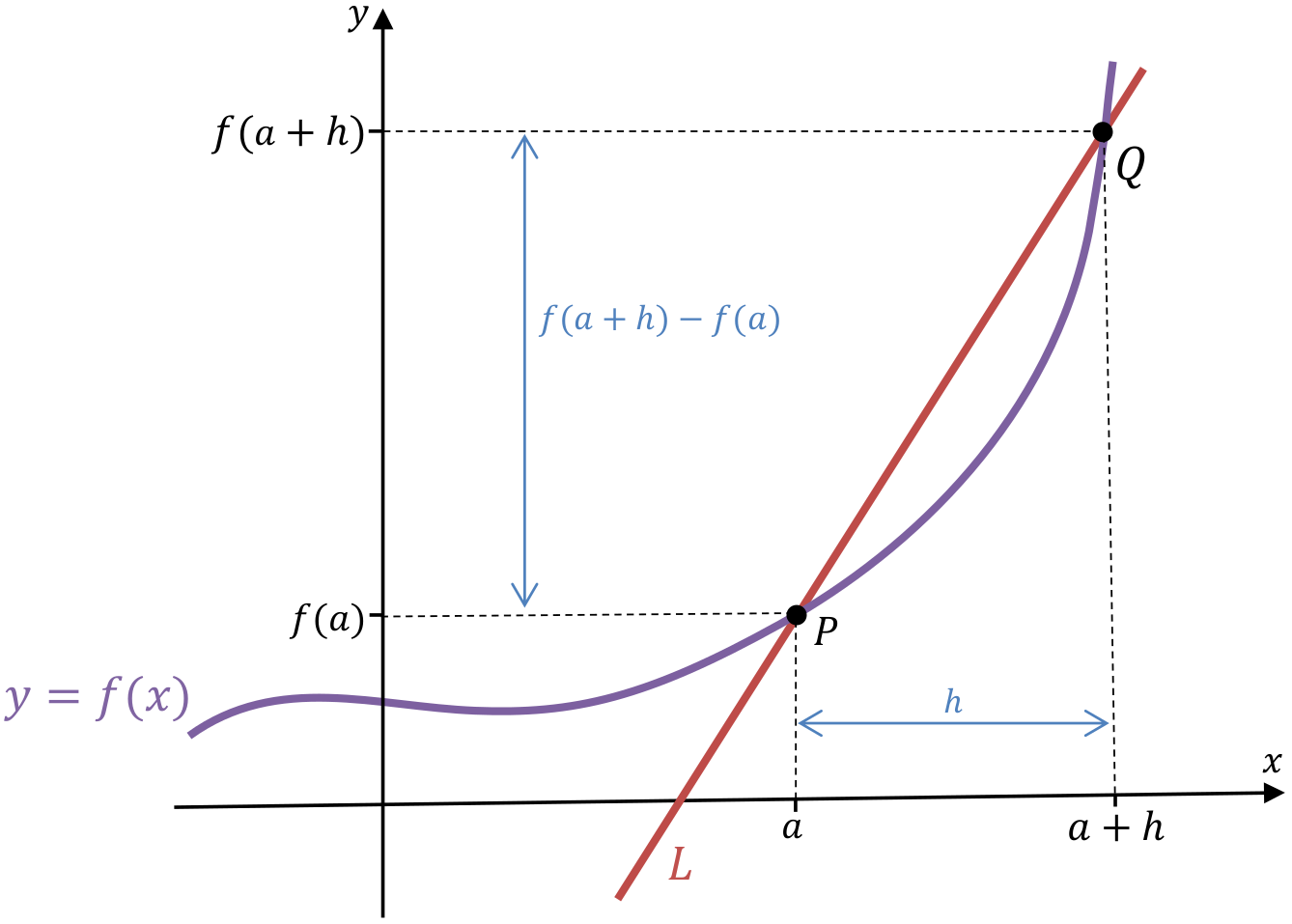
Provided and are very close together, the line passing through both of these points will give a good approximation for the tangent line at .
Suppose that and , where is a very small number.
The gradient of the straight line through and is given by the standard formula
As becomes very small, the point approaches , and becomes the tangent line at . The gradient of becomes the derivative of at , given by formula (1).
Differentiation using (1) is sometimes called differentiation by first principles.
Since we want to view the derivative as a funciton, we tend to use instead of in formula (1). Then, the derivative is given by
| (2) |
Example 2.
Differentiate from first principles.
Solution.
We use (2). Before we can evaluate the limit, we calculate for this particular function .
We have
Letting tend to zero, we then get
Exercise 3.
Let .
-
(i)
Calculate .
-
(ii)
Hence use (2) to differentiate from first principles.
Some Properties of Derivatives
Linearity Property
Differentiating Powers
Equation (3) may be used in conjunction with the linearity property for derivatives to differentiate any linear combination of powers of .
Example 4.
Use equation (3) to differentiate .
Solution.
First we rewrite the expression for using power notation:
By the linearity property for derivatives, we can calculate by differentiating term by term. Each term can be differentiating using the power rule (3). Hence
Exercise 5.
Use (3) to differentiate with respect to .