4. Differentiation#
4.1. Introduction#
The processes of differentiation and integration constitute the two corner–stones of the calculus which revolutionised mathematics (and its applications), starting from the groundbreaking work of Newton and Leibniz in the seventeenth century. In this chapter we will focus on understanding differentiation from a rigorous analytic viewpoint, using the knowledge that we have gained about limits of functions. Before we start this process let us remind ourselves what differentiation is for.
The geometric motivation for differentiation is to find the slope or gradient of the tangent to a curve at a point lying on it. If the curve is given by a formula \(y = f(x)\), then the gradient of the tangent at the point \((x, y)\) appears to be well–approximated by the slope of a chord connecting the very nearby points \((x, y)\) and \((x + \Delta x, y + \Delta y)\). This slope is given by the ratio:
But to get from the slope of the chord to the slope of the tangent, it seems that we must put \(\Delta x = 0\). This cannot be taken literally as it gives us the meaningless ratio \(0/0\).
The dynamic motivation for differentiation is to find the instantaneous rate of change of one quantity with respect to another. Let us assume that we are dealing with a physical quantity \(F(t)\) that changes as a function of time \(t\). For example \(F(t)\) could be position of a moving particle at time \(t\), in which case the required rate of change is the velocity. Or \(F(t)\) could be the charge on a conductor at time \(t\), in which case the rate of change is the current. Then over a very small time interval \(\Delta t\), the average rate of change is:
and we again want to understand what happens when \(\Delta t = 0\).
Of course, we now know that we must solve both of these problems by taking a limit as \(\Delta x\), or \(\Delta t\), tends to zero.
As before we will study real-valued functions defined on some subset \(A\) of the real numbers, \(f:A\to \mathbb{R}\).
4.2. Differentiation as a limit#
Definition 4.1
Let \(f:A\to\mathbb{R}\) be a function. We say that \(f\) is differentiable at \(a \in A\) if
has a well-defined limit as \(x\rightarrow a\). In this case we write
and we call \(f'(a) \in \mathbb{R}\), the derivative of \(f\) at \(a\).
We say that \(f\) is differentiable on \(S \subseteq A\) if it is differentiable at every point \(a \in S\).
The mapping \(a \mapsto f'(a)\) defines a real-valued function which is called the derivative of \(f\), and denoted by \(f'\). This has domain
Note that this definition involves the limit at \(a\) of the function
in the sense of Definition 2.2. Or, equivalently, the limit at \(0\) of the function \(h\mapsto \displaystyle\frac{f(a +h) - f(a)}{h}\).
In applied mathematics, we may often write \(y = f(x)\), and express the function \(f'\) as \(\frac{dy}{dx}\). Then \(f'(a) = \left.\frac{dy}{dx}\right|_{x=a}\). In analysis, this notation is not so helpful; it is usually easier to work with \(f'\).
We can of course, iterate the notion of differentiability in the usual way. Suppose that \(a \in \text{Dom}\left(f'\right)\) and that \(f'\) is differentiable at \(a\), then we define the second derivative \(f^{\prime \prime}(a)\) of \(f\) at \(a\) by
More generally if \(n\in\mathbb{N}\) with \(n > 2\) we define the \(n\)th derivative of \(f\) at \(a\) by
whenever the limit on the right-hand side exists. We say that \(f\) is infinitely differentiable or smooth at \(a\) if \(f^{(n)}(a)\) exists (and is finite) for all \(n\in\mathbb{N}\). It is also sometimes useful to employ the notation \(f(a) = f^{(0)}(a)\).
Example 4.1
If \(f:\mathbb{R}\to\mathbb{R}\) is given by \(f(x) = c\), where \(c\) in \(\mathbb{R}\) is constant, it is easy to check directly from Definition 4.1 that \(\text{Dom}\left(f'\right)= \mathbb{R}\), and \(f'(a) = 0\) for all \(a \in \mathbb{R}\).
Example 4.2
Let \(f:\mathbb{R}\to\mathbb{R}\) be given by \(f(x) = x^{n}\), where \(n\in\mathbb{N}\) is fixed. Use the Binomial Theorem to show directly from the definition that \(f\) is differentiable at all \(x\in\mathbb{R}\), with \(f'(x) = nx^{n-1}\).
Solution. Let \(a, h \in \mathbb{R}\). Using the binomial theorem, we have
Thus, using algebra of limits,
so \(f'(x) = nx^{n-1}\) for all \(x \in \mathbb{R}\), and \(\text{Dom}\left(f'\right) = \mathbb{R}\).
Next we turn our attention to the relationship between differentiability and continuity.
Theorem 4.1
If \(f:A\to\mathbb{R}\) is differentiable at \(a \in A\) then \(f\) is continuous at \(a\).
Proof. Using the definition of continuity (Definition 3.1), we need to show that \(\lim_{x\rightarrow a} f(x) = f(a)\). For \(x \neq a\), write
Since \(f\) is differentiable at \(a\), \(\displaystyle\lim_{x\rightarrow a} \displaystyle\frac{f(x) - f(a)}{x - a} = f'(a)\), and of course \(\displaystyle\lim_{x\rightarrow a} (x - a) = 0\). Hence by algebra of limits (Theorem 2.2),
So \(\displaystyle\lim_{x\rightarrow a}(f(x) - f(a))\) exists and equals zero, and the result follows, by algebra of limits again. \(\square\)
On the other hand, it is not true that every function that is continuous at \(a\) is differentiable at \(a\).
Example 4.3
Consider the function \(f:\mathbb{R}\to\mathbb{R}\) given by \(f(x) = |x|\). It is continuous at every point in \(\mathbb{R}\). It is also easy to see that it is differentiable at every \(x \neq 0\).
Show that \(f\) is not differentiable at zero, by showing that the relevant left and right limits are different there.
Solution (click to expand)
We have
Thus the left and right limits are different and so \(\lim_{h \to 0}\displaystyle\frac{f(0 + h) - f(0)}{h} \) does not exist.
Generalising the last example, we have the following definition.
Definition 4.2
We say that the function \(f:A\to\mathbb{R}\) has a left derivative at \(a \in A\) if the limit
exists, and that it has a right derivative at \(a \in A\) if the limit
exists.
Theorem 4.2
One can show that a function \(f:A\to \mathbb{R}\) is differentiable at \(a \in A\) if and only if both the left and right derivatives at \(a\) exist and are equal. In this case
4.3. Rules for differentiation#
The results in this section should all be familiar from MAS106. Howver, now we can make the proofs rigorous.
Theorem 4.3
Let \(f\) and \(g\) be real-valued functions that are differentiable at \(a \in \text{Dom}(f) \cap \text{Dom}(g)\). Then the following hold.
(i) For each \(\alpha,\beta \in \mathbb{R}\), the function \(\alpha f + \beta g\) is differentiable at \(a\) and
(ii) (The Product Rule) The function \(fg\) is differentiable at \(a\) and
(iii) (The Quotient Rule) If \(g(a) \neq 0\) then \(f/g\) is differentiable at \(a\) and
Proof. (i) We have
and, taking limits as \(h\) goes to \(0\), the result follows from the algebra of limits (Theorem 2.2).
(ii) For all \(h \neq 0\),
The result follows by taking limits as \(h \rightarrow 0\) and using Definition 4.1 and the algebra of limits, together with the fact that at \(a\), \(g\) is differentiable, hence continuous by Theorem 4.1, and so \(\lim_{h \rightarrow 0}g(a + h) = g(a)\). 3. First observe that by Problem 19, there exists \(\delta > 0\) such that \(g(x) \neq 0\) for all \(x \in (a - \delta, a + \delta)\). Consider \(h \in \mathbb{R}\) such that \(|h| < \delta\). Then
and the result follows by algebra of limits, taking the limit as \(h\) goes to \(0\), using the fact that (as above), \(\lim_{h \rightarrow 0}g(a + h) = g(a)\). \(\square\)
Theorem 4.4 (Chain rule)
Let \(f, g\) be real-valued functions such that the range of \(g\) is contained in the domain of \(f\). Suppose that \(g\) is differentiable at \(a\) and that \(f\) is differentiable at \(g(a)\). Then \(f \circ g\) is differentiable at \(a\) and
Proof. For \(x\in \text{Dom}(g)\), we consider
We would like to write this as
but that only makes sense when \(g(x)\neq g(a)\). To overcome this problem, we introduce the function \(Q:\text{Dom}(f)\to \mathbb{R}\) defined by
We claim that
for all \(x\in \text{Dom}(g)\). Indeed, for \(x\) such that \(g(x) \neq g(a)\), this is clear because the factors of \(g(x)-g(a)\) cancel. And for \(x\) such that \(g(x)=g(a)\), both sides are zero.
So we need to study
Since \(g\) is differentiable at \(a\), by Theorem 4.1, \(g\) is continuous at \(a\). Since \(f\) is differentiable at \(g(a)\), \(Q\) is continuous at \(g(a)\). So \(Q\circ g\) is continuous at \(a\) and \(\lim_{x\to a} Q(g(x))\) exists and is equal to \(Q(g(a))=f'(g(a))\). Using the algebra of limits, we then have
as required. \(\square\)
4.4. Turning points and Rolle’s theorem#
Definition 4.3
A function \(f:A\to\mathbb{R}\) has a local minimum at \(a \in A\) if there exists \(\delta > 0\) such that \((a-\delta, a+\delta)\subseteq A\) and \(f(x) \geq f(a)\) for all \(x \in (a-\delta, a+\delta)\).
A function \(f:A\to\mathbb{R}\) has a local maximum at \(a \in A\) if there exists \(\delta > 0\) such that \((a-\delta, a+\delta)\subseteq A\) and \(f(x) \leq f(a)\) for all \(x\in (a-\delta, a+\delta)\).
A turning point (sometimes called an extreme point}) for \(f\) is a point in its domain that is either a local minimum or a local maximum.
It is important to distinguish carefully between local maxima and minima and global maxima and minima, when the latter exist. For example if \(f:[a, b] \rightarrow \mathbb{R}\) is continuous, then we know by the extreme value theorem (Theorem 3.5) that it attains both its supremum and infimum on \([a, b]\). So these are the global maximum and minimum, respectively. But they are not necessarily turning points, because they might be at the endpoints of the interval \([a,b]\). And, of course, a local minimum/maximum need not be a global one.
Example 4.4
Consider the function \(f:[-3, 2] \rightarrow \mathbb{R}\) defined by
Identify any turning points and the global maximum and minimum.
Solution. Note that the function is continuous (by checking what happens at \(x=-1\)), so as above there is a global maximum and minimum. The global maximum is \(4\), attained at \(x = 2\). The global minimum is \(-1\), attained at \(x = -3\). Neither of these is a turning point (because they are the endpoints of the interval: we cannot find a \(\delta\) such that all points within distance \(\delta\) are contained in the domain). There is a local minimum at \(x = 0\) and a local maximum at \(x=-1\).
Theorem 4.5
If \(f:A\to\mathbb{R}\) is differentiable at \(a \in A\) and \(a\) is a turning point for \(f\), then \(f'(a) = 0\).
Proof. We suppose that \(f\) has a local minimum at \(a\). So there exists \(\delta > 0\) so that \((a-\delta, a+\delta)\subseteq\text{Dom}(f)\) and \(f(x) \geq f(a)\) for all \(x \in (a-\delta, a+\delta)\). Hence
Taking one-sided limits as \(x \rightarrow a\), we deduce that \(f_{-}'(a) \leq 0\) and \(f_{+}'(a) \geq 0\). But \(f\) is differentiable at \(a\), and so \(f_{-}'(a) = f_{+}'(a) = f'(a)\). We conclude that \(f'(a) = 0\), as required.
The argument in the case of a local maximum is very similar. \(\square\)
A point where a differentiable function has derivative zero is sometimes called a stationary point. So Theorem 4.5 says that turning points are stationary points. The converse to Theorem 4.5 is false: not all stationary points are turning points. Consider for example the familiar case of \(f(x) = x^{3}\). Then \(f'(0) = 0\) but \(0\) is neither a local maximum nor a local minimum; it is what is called an inflection point}. We will not pursue the story of classifying stationary points further here. You have seen this before in MAS106, and it is revisited in one of the exercises. Instead we will use Theorem 4.5 to explore some new territory.
Theorem 4.6 (Rolle’s theorem)
Let \(f:[a,b]\to\mathbb{R}\) be a function that is continuous on \([a,b]\) and differentiable on \((a,b)\) with \(f(a)=f(b)\). Then there exists \(c\in(a,b)\) such that \(f'(c) = 0\).
Proof. If \(f\) is constant, the result is obvious, so assume that \(f\) takes at least two distinct values. By Theorem 3.5, \(f\) is bounded on \([a, b]\) and attains both its supremum and infimum. It cannot attain both of these at the end-points, as then they would be equal and \(f\) would be constant. So there must be a \(c\in (a,b)\) where either the supremum or infimum is attained. But then \(c\) is a turning point, and so \(f'(c) = 0\) by Theorem 4.5. \(\square\)
4.5. The mean value theorem#
The next result is a generalisation of Rolle’s theorem and a very important result, with lots of interesting consequences.
Theorem 4.7 (Mean value theorem)
If \(f:[a,b]\to\mathbb{R}\) is continuous on \([a, b]\) and differentiable on \((a,b)\), then there exists \(c \in (a, b)\) such that
Proof. Let \(\alpha = \frac{f(b) - f(a)}{b - a}\). Define \(g:[a,b]\to\mathbb{R}\) by \(g(x) = f(x) - \alpha(x - a)\). Then \(g\) is continuous on \([a, b]\), and differentiable on \((a, b)\), because \(f\) is. You can check easily that \(g(a) = g(b) = f(a)\), and so we may apply Rolle’s theorem (Theorem 4.6) to deduce that there exists \(c \in (a, b)\) such that \(g^{\prime }(c) = 0\). But \(g'(c)=f'(c)-\alpha\) and hence \(f'(c) = \alpha\), as required. \(\square\)
The mean value theorem gives a rigorous foundation to the “geometrically obvious’’ assertion that a differentiable function \(f\) on an interval \([a, b]\) must at some point attain a slope equal to the slope of the line through the endpoints \((a, f(a))\) and \((b, f(b))\) — see Fig. 4.1.
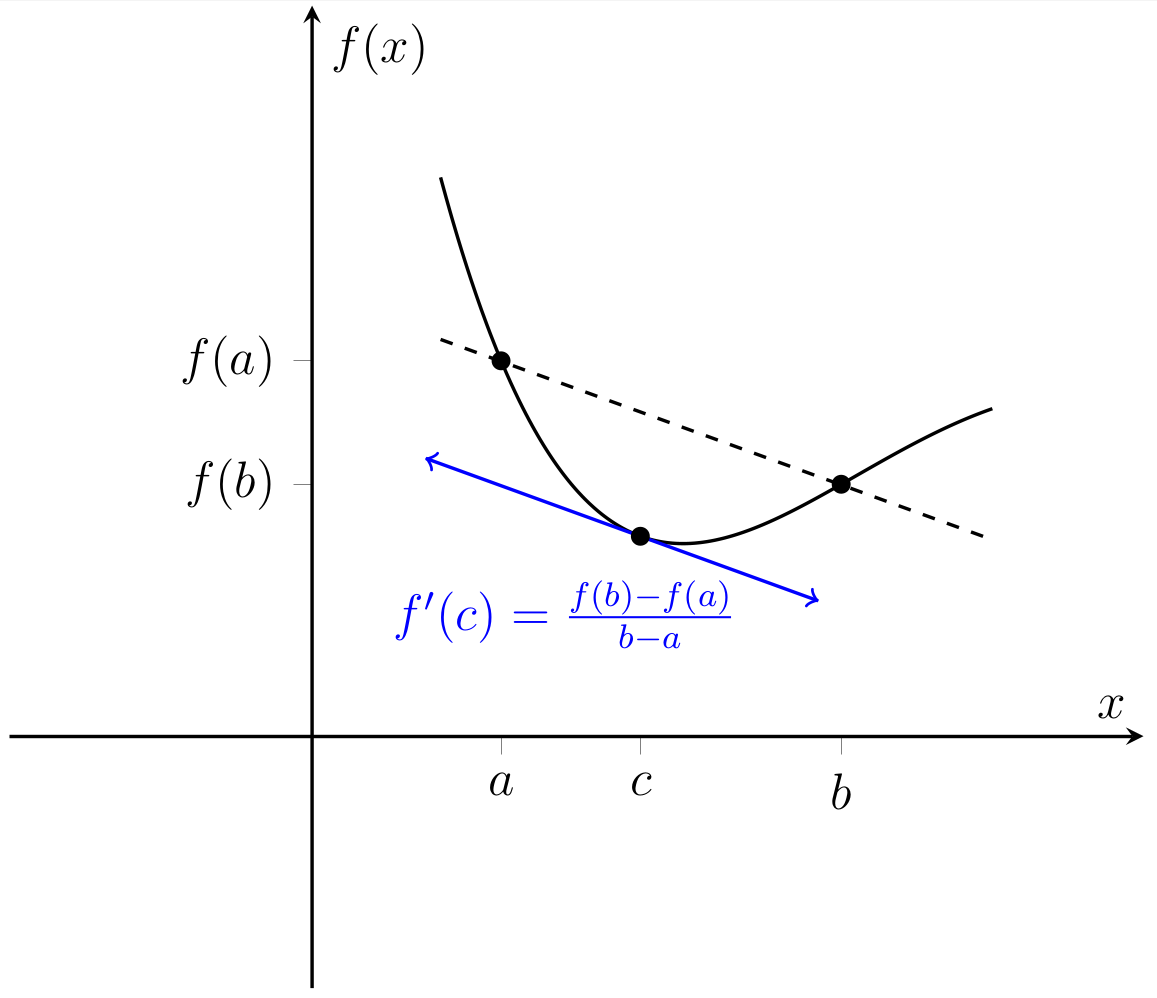
Fig. 4.1 A visual representation of the mean value theorem.#
In analysis, for any statement connecting calculus to some geometric property of a curve, the mean value theorem is likely to feature in its proof. We investigate one example of this next.
Corollary 4.1 (Monotonicity revisited)
Suppose that \(f:[a,b]\to\mathbb{R}\) is continuous on \([a, b]\) and differentiable on \((a, b)\).
(i) If \(f'(x) \geq 0\) for all \(x \in (a, b)\), then \(f\) is monotonic increasing on \([a, b]\).
(ii) If \(f'(x) > 0\) for all \(x \in (a, b)\), then \(f\) is strictly monotonic increasing on \([a, b]\).
(iii) If \(f'(x) \leq 0\) for all \(x \in (a, b)\), then \(f\) is monotonic decreasing on \([a, b]\).
(iv) If \(f'(x) < 0\) for all \(x \in (a, b)\), then \(f\) is strictly monotonic decreasing on \([a, b]\).
Proof. We’ll just do the first of these, as the others are so similar. Choose arbitrary \(\alpha, \beta\) such that \(a \leq \alpha < \beta \leq b\). By the mean value theorem (Theorem 4.7), there exists \(c \in (\alpha, \beta)\) so that
Hence \(f(\beta) \geq f(\alpha)\) and so \(f\) is monotonic increasing, as required. \(\square\)
