Sequences and series of functions — Non-examinable 2024–25

5. Sequences and series of functions — Non-examinable 2024–25#

In this chapter we will study sequences and series of functions. We start by considering two different notions of convergence for a sequence of functions. Later we will consider the interaction between continuity and these notions of convergence, as well as looking at differentiation. The results we obtain for sequences of functions will later be applied to series of functions, by considering sequences of partial sums.

5.1. Pointwise and uniform convergence#

Let $X\subseteq\mathbb{R}$, and consider a sequence of functions, $(f_n)$, where $f_n:X\rightarrow \mathbb{R}$ for each $n\in\mathbb{N}$.

Definition 5.1

We say the sequence $(f_n)$ converges pointwise to a function $f:X\rightarrow \mathbb{R}$ if for each $x\in X$, we have

\[ \lim_{n\rightarrow \infty} f_n(x) = f(x) . \]

In other words, the sequence $(f_n)$ converges pointwise to $f$ if for each $x\in X$ and $\varepsilon >0$, there exists $N\in \mathbb{N}$ such that $|f_n(x) -f(x)|<\varepsilon$ whenever $n\geq N$.

Note that in this definition, the $N$ can depend not just on the value of $\varepsilon$, but also on the point $x$. The sequence $(f_n(x))$ may converge much quicker for some values of $x$ and much slower for others — all we know is that it will eventually converge to $f(x)$, for each fixed $x$.

Example 5.1

Define $f_n:[0,2\pi ] \rightarrow \mathbb{R}$ by $f_n(x) = \cos (x/n)$. Show that the sequence $(f_n)$ converges pointwise and determine the limit function.

Solution. Observe that $\frac{x}{n}\rightarrow 0$ as $n\rightarrow \infty$, and $\cos$ is a continuous function, so for each $x\in [0,2\pi ]$, we have

\[ \cos \left( \frac{x}{n} \right) \rightarrow \cos 0 =1 \]

as $n\rightarrow \infty$. Thus the sequence $(f_n)$ has pointwise limit the constant function $f:[0,2\pi ] \rightarrow \mathbb{R}$, with $f(x)=1$ for all $x\in [0,2\pi]$.

Example 5.2

Define $f_n:[0,2]\rightarrow \mathbb{R}$ by $f_n(x) =x^n$. Show that the sequence $(f_n)$ does not converge pointwise.

Solution. Note that if $x>1$, then $x^n\rightarrow \infty$ as $n\rightarrow \infty$, so if $x>1$ then

\[ \lim_{n\rightarrow \infty} f_n (x) \]

does not exist, and $(f_n)$ has no pointwise limit.

Example 5.3

Define $f_n :[0,1]\rightarrow \mathbb{R}$ by $f_n(x)=x^n$. Show that the sequence $(f_n)$ converges pointwise and determine the limit function.

Solution. Now that the domain has been restricted to $[0,1]$, we do not need to worry about $x^n$ becoming unbounded as $n\rightarrow\infty$. We treat the cases $x<1$ and $x=1$ separately. For $x<1$,

\[ f_n(x) = x^n\rightarrow 0 \]

as $n\rightarrow \infty$.

On the other hand, $f_n(1) = 1^n =1$ for all $n$, so $f_n(1)\rightarrow 1$ as $n\rightarrow \infty$. Hence the sequence $(f_n)$ converges pointwise, with pointwise limit

\[\begin{split} f:[0,1]\to\mathbb{R}; \; f(x) = \left\{ \begin{array}{ll} 0 & x<1, \\ 1 & x=1. \\ \end{array} \right. \end{split}\]

5.1.1. Uniform convergence#

It is natural to wonder what conditions are necessary for “nice’’ properties such as continuity to be preserved in the limit as $n\rightarrow\infty$. Example 5.3 shows that pointwise convergence alone is not enough: we had a sequence of continuous functions converging pointwise to a limit that was not continuous.

Recall when we defined pointwise convergence of a sequence $(f_n)$ to a funciton $f$, we noted that $(f_n(x))$ may converge faster for some values of $x$ than others. This is the issue that led to the development of uniform convergence: a notion of convergence that requires the sequence of functions to converge at the same rate at every point. We shall see that uniform convergence is a much stronger condition than pointwise convergence, and preserves such things as continuity and to an extent differentiation.

Definition 5.2

Let $X\subseteq\mathbb{R}$ and $f_n:X\rightarrow \mathbb{R}$ for each $n\in\mathbb{N}$. We say the sequence $(f_n)$ converges uniformly to a function $f:X\rightarrow \mathbb{R}$ when for all $\varepsilon >0$, we have $N\in \mathbb{N}$ such that $|f_n(x) -f(x)|<\varepsilon$ for all $n\geq N$ and $x\in X$.

The difference between this definition and pointwise convergence is that the $N$ does not depend on the point $x$, only on $\varepsilon$. This can be seen more starkly by expressing their definitions in terms of quantifiers:

$f_n\rightarrow f$ uniformly if and only if

(5.1)#\[\forall\epsilon>0 \; \exists N\in\mathbb{N} \text{ s.t. } \forall n\geq N\; \forall x\in X \; |f_n(x)-f(x)|<\epsilon.\]

$f_n\rightarrow f$ pointwise if and only if

(5.2)#\[\forall x\in X \; \forall\epsilon>0 \; \exists N\in\mathbb{N} \text{ s.t. } \forall n\geq N \; |f_n(x)-f(x)|<\epsilon.\]

In (5.2), $x$ dependence is introduced at the very start, and may affect our choice of $N$. Meanwhile, in (5.1), $x$ does not appear until the very end, and our choice of $N$ will work for all values of $x$. The definitions are identical in all other regards.

In particular we have the following:

Proposition 5.1

If $f_n\rightarrow f$ uniformly, then $f_n\rightarrow f$ pointwise.

That is, uniform convergence implies pointwise convergence, and when both hold, the limit functions are the same. This will be useful later when proving sequences are uniformly convergent, as we can identify the intended limit function by first computing the pointwise limit.

First, we prove an equivalent characterisation of uniform convergence, that is typically easier to use in practice than Definition 5.2

Proposition 5.2

Consider a sequence of functions $f_n :[a,b]\rightarrow \mathbb{R}$. Let $f:[a,b]\rightarrow \mathbb{R}$. Then the following statements are equivalent.

(i) The sequence $(f_n)$ converges uniformly to $f$.

(ii) Let $M_n = \sup \{ |f_n (x) -f(x) : x\in [a,b] \}$. Then $M_n \rightarrow 0$ as $n\rightarrow \infty$.

Proof. Let $(f_n)$ converge uniformly to $f$.

Let $\varepsilon >0$. Then we have $N\in \mathbb{N}$ such that $|f_n(x)-f(x)|<\frac{\varepsilon}{2}$ whenever $n\geq N$, for all $x\in [a,b]$. Let $n\geq N$. Then

\[ M_n = \sup \{ |f_n(x) -f(x)| : x\in [a,b] \} \leq \frac{\varepsilon}{2} < \varepsilon. \]

Thus $M_n\rightarrow 0$ as $n\rightarrow \infty$, and the second condition holds.

Conversely, suppose $M_n \rightarrow 0$ as $n\rightarrow \infty$. Let $\varepsilon >0$. Then we have $N\in \mathbb{N}$ such that $M_n < \varepsilon$ whenever $n\geq N$. But this means, for $n\geq N$, that

\[ \sup_{x\in [a,b]} |f_n(x)-f(x)| <\varepsilon \]

and so $|f_n(x) -f(x)|<\varepsilon$ whenever $n\geq N$, for all $x\in [a,b]$. Thus $(f_n)$ converges to $f$ uniformly, as required. $\square$

The condition on the $M_n$s in Proposition 5.2 is usually the easiest way to actually prove uniform convergence in an example.

Example 5.4

For $n\geq 2$, define $f_n :[0,2\pi ]\rightarrow \mathbb{R}$ by

\[ f_n(x) = \frac{1-2n}{1-n} \sin(x). \]

First show that the sequence $(f_n)$ converges pointwise and determine the limit function $f$. Then show that in fact the sequence $(f_n)$ converges uniformly to $f$.

Solution. Observe that

\[ f_n(x) = \frac{ \frac{1}{n}-2}{\frac{1}{n}-1 } \sin(x) \rightarrow 2\sin(x) \]

as $n\rightarrow \infty$, so $(f_n)$ converges pointwise to $f:[0,2\pi]\rightarrow\mathbb{R}$; $f(x) =2\sin(x)$.

We now show that $f_n\rightarrow f$ uniformly.

\[ |f_n(x)-f(x) | = \left| \frac{1-2n}{1-n} -2 \right| |\sin(x) | \leq \left| \frac{1-2n}{1-n} -2 \right| \]

for all $x\in[0,2\pi]$, and

\[ \left| \frac{1-2n}{1-n} -2 \right| = \frac{1}{n-1}\rightarrow 0, \hspace{1em} \text{ as } n\rightarrow \infty. \]

Thus, if

\[ M_n = \sup \{ |f_n (x) -f(x)| : x\in [0,2\pi ] \} \]

then $0\leq M_n \leq \frac{1}{n-1}$. And since $\frac{1}{n-1}\rightarrow 0$ as $n\rightarrow \infty$, we have $M_n\rightarrow 0$ as $n\to \infty$. So $(f_n)$ converges uniformly to $f$, by Proposition 5.2.

5.1.2. General procedure for calculating uniform limits#

Example 5.4 demonstrates an approach that is typically the best way to prove or check for uniform convergence.

To prove a sequence of functions $(f_n)$ converges uniformly:

Calculate its pointwise limit, $f$.
Prove that $f_n$ also converges to $f$ uniformly, using Proposition 5.2 or Definition 5.2.

5.2. Continuity and differentiability under uniform limits#

We are now ready to prove that continuity is preserved by uniform limits.

Theorem 5.1 (Uniform limit theorem)

Let $f_n :X\rightarrow \mathbb{R}$ be continuous for each $n\in \mathbb{N}$. Suppose the sequence $(f_n)$ converges uniformly to a function $f:X\rightarrow \mathbb{R}$. Then $f$ is continuous.

Proof. Let $x_0\in X$. We want to prove that $f$ is continuous at $x_0$. We’ll use the $(\varepsilon-\delta)$ criterion for continuity.

Let $\varepsilon >0$. Then since $(f_n)$ converges uniformly to $f$, there is $N\in \mathbb{N}$ such that

(5.3)#\[|f_n(x)-f(x)|<\frac{\varepsilon}{3},\]

for all $x\in X$ and all $n\geq N$.

Since $f_N$ is continuous at $x_0$, we can find $\delta >0$ such that

(5.4)#\[|f_N(x) - f_N(x_0)|< \frac{\varepsilon}{3}\]

whenever $|x-x_0|<\delta$.

Let $x\in X$ be such that $|x-x_0|<\delta$. Then using the triangle inequality together with (5.3) and (5.4),

\[\begin{align*} |f(x)-f(x_0)| &\leq |f(x) -f_N(x)| + |f_N(x)-f_N(x_0)| + |f_N (x_0) - f(x_0)| \\ &< \frac{\varepsilon}{3} + \frac{\varepsilon}{3} + \frac{\varepsilon}{3} = \varepsilon. \end{align*}\]

Thus $f$ is continuous at $x_0$. Since $x_0$ was arbitrary, we conclude that $f$ is a continuous funciton. $\square$

Remark. The proof of Theorem 5.1 is sometimes called the “$\varepsilon/3$ proof” because of the main trick.

Example 5.5

Let $f_n : [0,1]\to\mathbb{R}$ be given by $f_n(x) =x^n$. Show that the sequence $(f_n)$ does not converge uniformly.

Solution. We saw in Example 5.3 that the sequence $(f_n)$ has pointwise limit $f$, where

\[\begin{split} f(x) = \left\{ \begin{array}{ll} 0 & x<1, \\ 1 & x=1.\\ \end{array} \right. \end{split}\]

If $(f_n)$ did converge uniformly the limit would have to be this function $f$. But $f$ is clearly not continuous at $x=1$. So $(f_n)$ does not converge uniformly.

The power of uniform limits extends beyond just continuity. We state a version of the uniform limit theorem for differentiability. Its proof is non-examinable but included in the appendix for interest — see Section A.2.

Theorem 5.2 (Differentiable limit theorem)

Consider differentiable functions $f_n:[a,b]\rightarrow \mathbb{R}$. Suppose that

(i) $(f_n)$ converges pointwise to a function $f$, (ii) Each derivative $f_n'$ is continuous, and (iii) The sequence of derivatives $(f'_n)$ converges uniformly to a function $g$.

Then $f$ is differentiable, and $f'=g$.

Proof. See Section A.2 in the Appendix.

Thus we can, under suitable conditions, swap limits and differentiation.

The following example shows that convergence conditions on the sequence of derivatives are necessary.

Example 5.6

Define $f_n\colon [0,2\pi ]\rightarrow \mathbb{R}$ by

\[ f_n (x) = \frac{1}{n} \sin (n^2 x) . \]

Show that $(f_n)$ converges uniformly to the zero function, but $(f_n')$ does not converge pointwise.

Solution. Observe that $|f_n(x)|\leq \frac{1}{n}$ for all $x\in [0,2\pi ]$, and $\frac{1}{n}\rightarrow 0$ as $n\rightarrow \infty$. Thus the sequence $(f_n)$ converges uniformly to $0$, the zero function.

But

\[ f_n'(x) =n\cos (n^2 x) \]

and the sequence $(f_n')$ does not converge pointwise (let alone uniformly).

5.3. Series of functions#

We can treat convergence of series of functions via sequences of partial sums. This mirrors the approach taken for series of real numbers, as seen in MAS107.

Definition 5.3

Let $X\subseteq\mathbb{R}$, and let $(f_n)$ be a sequence of functions, with $f_n:X\rightarrow \mathbb{R}$ for each $n\in\mathbb{N}$. We consider the sequence of partial sums $(s_n)$, where $s_n:X\rightarrow \mathbb{R}$ is defined by

\[ s_n(x)=f_1(x)+f_2 (x) + \cdots +f_n (x). \]

We say the infinite series $\sum_{n=1}^\infty f_n$ converges pointwise if $(s_n)$ converges pointwise. In other words, $\sum_{n=1}^\infty f_n$ converges pointwise if, for each $x\in X$, the series $\sum_{n=1}^\infty f_n(x)$ converges.

We say that the sequence $(f_n)$ is uniformly summable}, or that the series $\sum_{n=1}^\infty f_n$ converges uniformly on $X$ if the sequence $(s_n)$ of partial sums converges uniformly.

Theorem 5.1 and Theorem 5.2 immediately give us the following two results.

Theorem 5.3

Let $(f_n)$ be a uniformly summable sequence of continuous functions $f_n :X\rightarrow \mathbb{R}$. Then the function

\[ f:X\rightarrow \mathbb{R}; \; f(x) = \sum_{n=1}^\infty f_n (x) \]

is continuous.

Theorem 5.4

Let $(f_n)$ be a sequence of differentiable functions, $f_n :[a,b]\rightarrow \mathbb{R}$, such that the series $\sum_{n=1}^\infty f_n$ converges pointwise to a function $f$, each $f_n'$ is continuous and the series $\sum_{n=1}^\infty f_n'$ is uniformly convergent.

Then $f$ is differentiable and

\[ f'(x) = \sum_{n=1}^\infty f_n'(x) \]

for all $t\in [a,b]$.

In order for the above to be useful, we need a criterion for uniform convergence of a series. The following result, called the Weierstrass $M$-test provides a handy criterion.

Theorem 5.5 (Weierstrass $M$-test)

Let $f_n :X\rightarrow \mathbb{R}$ be a sequence of functions. Suppose we have a summable sequence of real numbers $(M_n)$ such that $|f_n (x)| \leq M_n$ for all $n$, and all $x\in X$.

Then the sequence $(f_n)$ is uniformly summable, and $\sum_{n=1}^\infty f_n (x)$ converges absolutely for each $x\in X$.

Proof. For each $x\in X$, absolute convergence of the series

\[ \sum_{n=1}^\infty f_n (x) \]

follows immediately from the comparison test for infinite series[1].

Let $(s_n)$ again denote the sequence of partial sums, so that $s_n=\sum_{k=1}^nf_k(x)$ for each $n\in\mathbb{N}$. We have established pointwise convergence of $(s_n)$ to the function

\[ s:X\to\mathbb{R}; \; s(x)=\sum_{n=1}^\infty f_n (x). \]

We will show that $s_n\rightarrow s$ uniformly. Let $\varepsilon >0$. Since the series $\sum_{n=1}^\infty M_n$ converges, we may choose $N\in\mathbb{N}$ such that $\sum_{k=n+1}^\infty M_k < \varepsilon$ whenever $n\geq N$.

Then, for all $n\geq N$ and $x\in X$,

\[ |s(x) - s_n(x) | = \left| \sum_{k=n+1}^\infty f_n (x) \right| \leq \sum_{k=n+1}^\infty |f_k (x)| \leq \sum_{k=n+1}^\infty M_k <\varepsilon. \]

Since this holds for all $x\in X$, it follows that $s_n\rightarrow s$ uniformly. So $(f_n)$ is uniformly summable. $\square$

The Weierstrass $M$-test is very useful for defining functions via their power series. In particular, we are now in a position to begin a rigorous treatment of the exponential function.

Example 5.7 (Exponential function)

Let $R>0$, and for $n\in\mathbb{N}$, define

\[ f_n:[-R,R]\to\mathbb{R}; \hspace{1em} f_n(x) = \frac{x^n}{n!}. \]

Then for $x\in[-R,R]$, $|f_n(x)|\leq\frac{R^n}{n!}$. Let $M_n=\frac{R^n}{n!}$. Since $M_n>0$ for all $n$, we can apply the ratio test to see if $M_n$ is a summable sequence of real numbers.

The ratio test[2] asks us to consider the behaviour of $\frac{M_{n+1}}{M_n}$ as $n\rightarrow\infty$. If this limit exists, there are three possible scenarios:

If $\displaystyle\lim_{n\rightarrow\infty}\frac{M_{n+1}}{M_n}<1$, then $\sum_{n=0}^\infty M_n$ converges.
If $\displaystyle\lim_{n\rightarrow\infty}\frac{M_{n+1}}{M_n}>1$, then $\sum_{n=0}^\infty M_n=+\infty$.
If $\displaystyle\lim_{n\rightarrow\infty}\frac{M_{n+1}}{M_n}=1$, then the test is inconclusive.

Now,

\[ \frac{M_{n+1}}{M_n} = \frac{R^{n+1}n!}{(n+1)!R^n} = \frac{R}{n+1}\rightarrow 0 \hspace{1em} \text{ as } n\rightarrow \infty. \]

Since this limit is strictly less than 1, we can conclude that the sequence $M_n$ is summable. By Theorem 5.5, $(f_n)$ is uniformly summable.

$R$ was chosen arbitrarily, and so we can define a mapping $\exp:\mathbb{R}\to\mathbb{R}$ by

\[ \exp(x) = \sum_{n=0}^\infty \frac{x^n}{n!}, \]

and this series converges uniformly on bounded intervals. Each term is continuous, and so by Theorem 5.3 so is $\exp$. Each term is also differentiable, so by Theorem 5.4, $\exp$ is differentiable and can be differentiated term by term. Thus

\[ \exp'(x) = \sum_{n=1}^\infty\frac{t^{n-1}}{(n-1)!} = \exp(x). \]

But then $\exp$ is infinitely differentiable, and we have established one of the key properties of the exponential function!

Further rigorous development of the exponential function, including a proof that $\exp(x)=e^x$, can be found in appendix Section A.3, for interest[3].

The Weierstrass $M$-test can also be used to construct examples with pathological properties.

Proposition 5.3

There is a function $f:\mathbb{R} \rightarrow \mathbb{R}$ which is continuous everywhere, but differentiable nowhere.

Proof. (Sketch)

Define a function $f_n :\mathbb{R} \rightarrow \mathbb{R}$ by

\[ f_n (x) = \frac{1}{10^n} \left(\text{distance from $10^n x$ to the nearest integer}\right). \]

Note that $f_n$ can also be expressed using the $\text{round}$ function, which rounds a given input to the nearest integer. We have

\[ f_n(x) = \frac{\left|10^nx - \text{round}(10^nx)\right|}{10^n}. \]

Let $f=\sum_{n=1}^\infty f_n$.
Use the Weierstrass $M$-test to show that the series $\sum_{n=1}^\infty f_n$ converges uniformly.
Apply the Uniform Limit Theorem (Theorem 5.1) to show that $f$ is continuous.
Check directly that $f$ is not differentiable anywhere, by showing that the required limit does not exist. (To give full details of this is quite long. But the idea is straightforward: $f_1$ has “corners’’ at $\frac{n}{20}$ for $n\in\mathbb{Z}$, $f_2$ has “corners’’ at $\frac{n}{200}$ for $n\in\mathbb{Z}$ and so on - thus $f$ has “corners’’ everywhere and is differentiable nowhere.) ”$\square$”

The graph of $y=f(x)$ is extremely jagged, as might be expected from a nowehere differentiable continuous function.

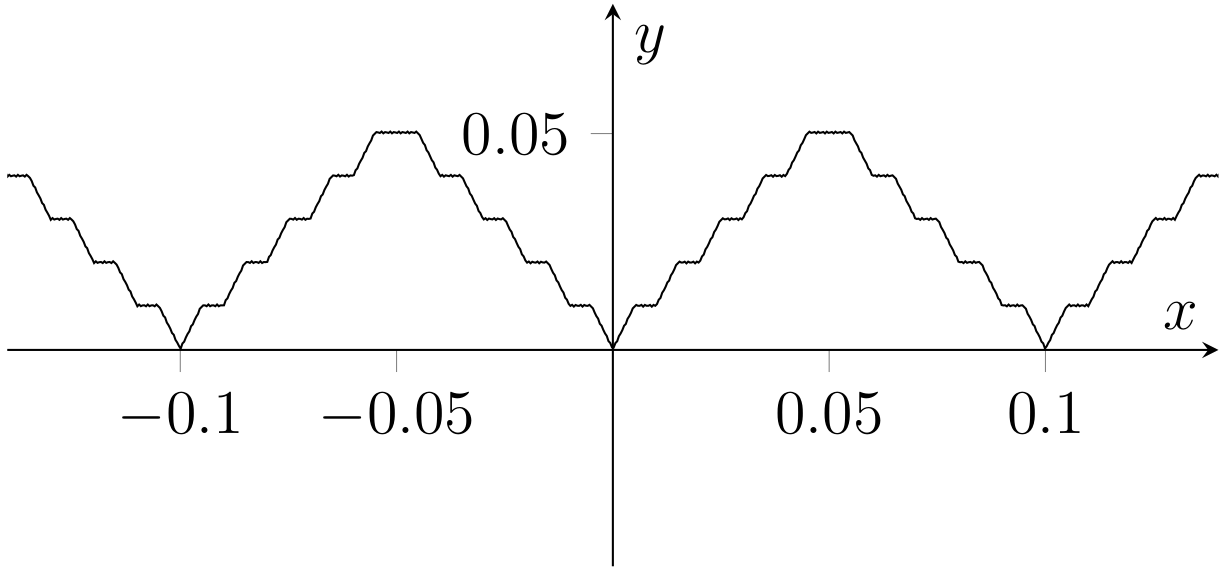
_images/NDcts.png — Fig. 5.1 Graph of $f$.#

For an interactive version of this graph, try this desmos link.

Examples of continuous nowhere differentiable functions have been known about since the late 19th century, though they were typically met with derision. Henri Poincaré famously described them as “monsters’’ and called Weierstrass’ work “an outrage against common sense’’, while Charles Hermite wrote that they were a “lamentable scourge’’.

More recent developments in mathematics have produced examples of continuous nowhere differentiable functions that occur in the natural world, such as the probabilistic model for Brownian motion.